Creating your first Geometry

This is a tutorial that shows you how to create a simple geometry.

import numpy as np
import matplotlib.pyplot as plt
import tofu.geom as tfg

Creating an empty Vessel

If a vessel object does not exist yet, you have to create one (otherwise you can just load an existing one). A vessel object is basically defined by a 2D simple polygon (i.e.: non self-intersecting), that is then expanded linearly or toroidally depending on the desired configuration. This polygon limits the volume available for the plasma, where the emissivity can be non-zero. It is typically defined by the inner wall in a tokamak.

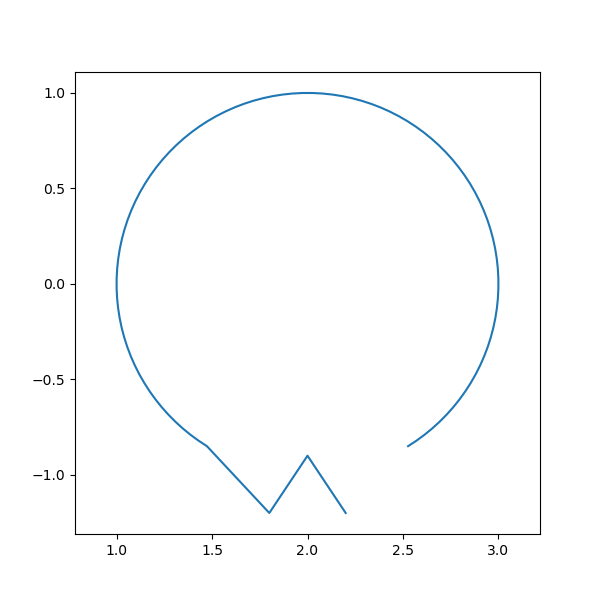
Let’s define the polygon limiting the vessel as a circle with a divertor-like shape at the bottom:

# Define the center, radius and lower limit
R0, Z0, rad, ZL = 2.0, 0.0, 1.0, -0.85
# Define the key points in the divertor region below ZL
Div_R, Div_Z = [R0 - 0.2, R0, R0 + 0.2], [-1.2, -0.9, -1.2]
# Find the angles corresponding to ZL and span the rest
thet1 = np.arcsin((ZL - Z0) / rad)
thet2 = np.pi - thet1
thet = np.linspace(thet1, thet2, 100)
# Assemble the polygon
poly_R = np.append(R0 + rad * np.cos(thet), Div_R)
poly_Z = np.append(Z0 + rad * np.sin(thet), Div_Z)
# Plot for checking
plt.figure(facecolor="w", figsize=(6, 6))
plt.plot(poly_R, poly_Z)
plt.axis("equal")

Out:

(0.900292944643613, 3.099707055356387, -1.3099829327148826, 1.1096415870125362)

Notice that the polygon does not have to be closed, ToFu will anyway check that and close it automatically if necessary. Now let’s feed this 2D polygon to the appropriate ToFu class and specify that it should be a toroidal type (if linear type ‘Lin’ is chosen, the length should be specified by the ‘Lim’ keyword argument). tofu also asks for a name to be associated to this instance, and an experiment (‘Exp’) and a shot number (useful when the same experiment changes geometry in time).

# Create a toroidal Ves instance with name 'MyFirstVessel', associated to
# the experiment 'Misc' (for 'Miscellaneous') and shot number 0
ves = tfg.Ves(
    Name="MyFirstVessel",
    Poly=[poly_R, poly_Z],
    Type="Tor",
    Exp="Misc",
    shot=0
)

Now the vessel instance is created. It provides you several key attributes and methods (see geom for details). Among them the Id attribute is itself a class instance that contains all useful information about this vessel instance for identification, saving… In particular, that’s where the name, the default saving path, the Type, the experiment, the shot number… are all stored. A default name for saving was also created that automatically includes not only the name you gave but also the module from which this instance was created (tofu.geom or tfg), the type of object, the experiment, the shot number… This recommended default pattern is useful for quick identification of saved object, it is advised not to modify it.

print(ves.Id.SaveName)

Out:

TFG_Ves_ExpMisc_MyFirstVessel_sh00000_Vers1.5.0-3-g96c1c10c

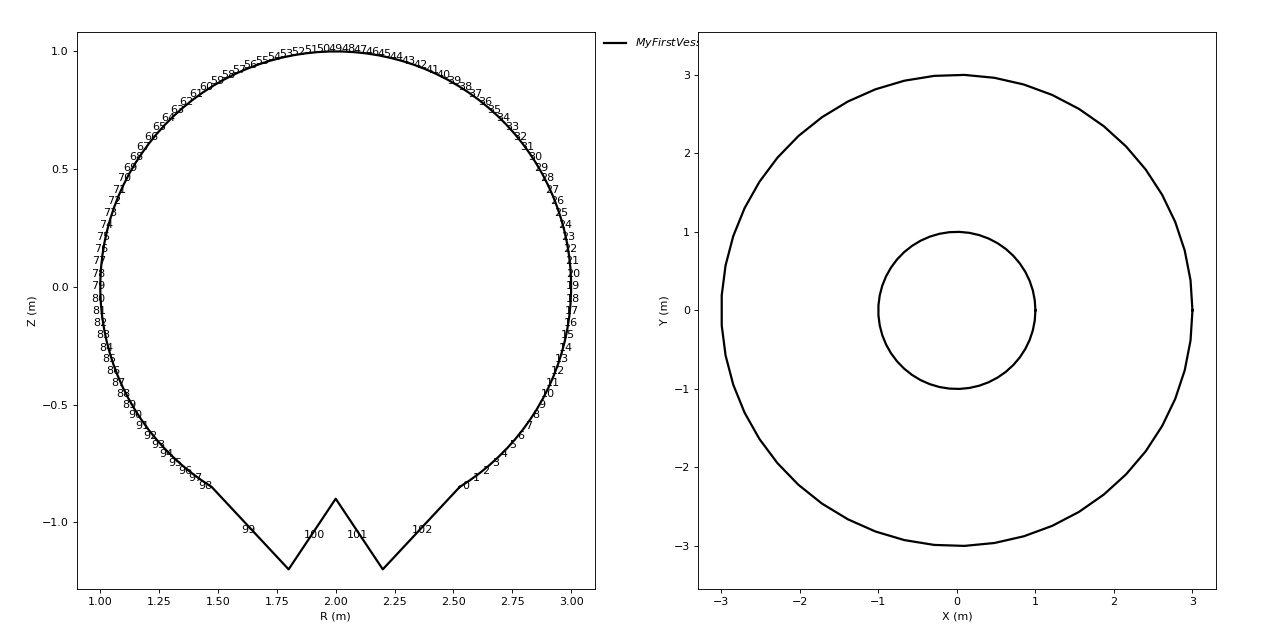
Now, we can simply visualise the created vessel by using the dedicated method (keyword argument ‘Elt’ specifies the elements of the instance we want to plot, typically one letter corresponds to one element, here we just want the polygon):

# Plot the polygon by default in two projections (cross-section and horizontal)
# and return the list of axes
lax = ves.plot(element="P")

Out:

/home/lasofivec/tofu/tofu/geom/_def.py:127: MatplotlibDeprecationWarning:
The set_window_title function was deprecated in Matplotlib 3.4 and will be removed two minor releases later. Use manager.set_window_title or GUI-specific methods instead.
  f.canvas.set_window_title(wintit)

The created vessel instance, plotted in cross-section and horizontal projections Since the vessel is an important object (it defines where the plasma lives), all the other ToFu objects rely on it. It is thus important that you save it so that it can be used by other ToFu objects when necessary.

ves.save(path="./")

Out:

Saved in :
    /home/lasofivec/tofu/examples/tutorials/TFG_Ves_ExpMisc_MyFirstVessel_sh00000_Vers1.5.0-3-g96c1c10c.npz

This method will save the instance as a numpy compressed file (.npz), using the path and file name found in ves.Id.SavePath and ves.Id.SaveName. While it is highly recommended to stick to the default value for the SaveName, but you can easily modify the saving path if you want by specifying it using keyword argument Path.

Adding structural elements

Like for a vessel, a structural element is mostly defined by a 2D polygon. If a vessel instance is provided, the type of the structural element (toroidal or linear) is automatically the same as the type of the vessel, otherwise the type must be specified.

# A configuration, short for geometrical configuration is a set of vessel,
# and structural elements.

# Define two polygons, one that does not enclose the vessel and one that does
thet = np.linspace(0.0, 2.0 * np.pi, 100)
poly1 = [[2.5, 3.5, 3.5, 2.5], [0.0, 0.0, 0.5, 0.5]]  # a rectangle
poly2 = [R0 + 0.5 * np.cos(thet), -1.0 + 0.5 * np.sin(thet)]  # a circle
poly3 = [[0.8, 1.3, 1.3, 0.8], [-0.5, -0.5, 0.5, 0.5]]  # another rectangle
# Create the structural elements with the appropriate ToFu class, specifying
# the experiment and a shot number for keeping track of changes
s1 = tfg.PFC(Name="S1",
             Poly=poly1,
             Exp="Misc",
             shot=0)
# now we create a structure that is not continuous along phi
# but is only defined within certain limits
s2 = tfg.PFC(
    Name="S2",
    Poly=poly2,
    Exp="Misc",
    shot=0,
    Lim=[[0.0, np.pi], [np.pi / 2.0, np.pi * 3.0 / 2.0]],
)
# and another one, now defined as repetitions centered a position `pos`
# and with a certain `extent`
# here we wanted a structure uniformly repeated 5 times along phi
s3 = tfg.PFC(
    Name="S3",
    Poly=poly3,
    # we dont take the last element of the list as it is 2.*pi = 0
    pos=np.linspace(0.0, 2.0 * np.pi, 6)[:-1],
    # 5 repetitions + 5 empty spaces = 10 subdivision of 2. pi
    extent=np.pi * 2.0 / 10.0,
    Exp="Misc",
    shot=0,
)
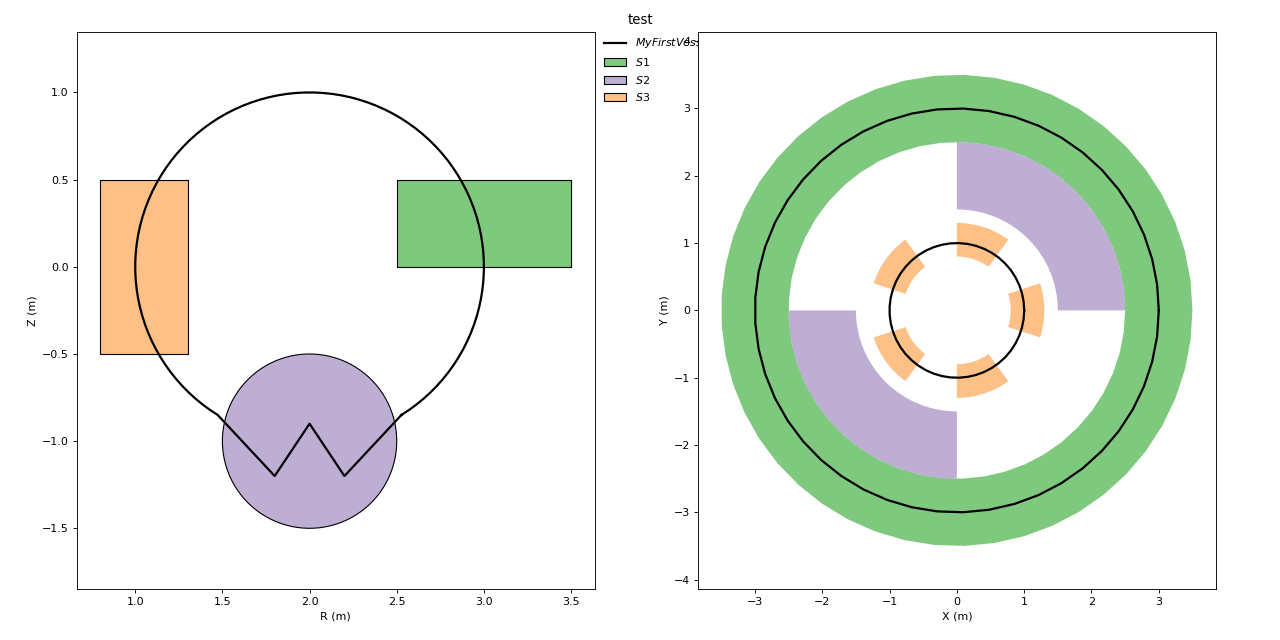
# Creating a configuration with vessel and structures
config = tfg.Config(Name="test",
                    Exp="Misc",
                    lStruct=[ves, s1, s2, s3])
config.set_colors_random()  # to see different colors
config.plot()
config.save()
# sphinx_gallery_thumbnail_number = 3

Out:

/home/lasofivec/tofu/tofu/geom/_def.py:127: MatplotlibDeprecationWarning:
The set_window_title function was deprecated in Matplotlib 3.4 and will be removed two minor releases later. Use manager.set_window_title or GUI-specific methods instead.
  f.canvas.set_window_title(wintit)
Saved in :
    /home/lasofivec/tofu/doc/source/TFG_Config_ExpMisc_test_sh00000_Vers1.5.0-3-g96c1c10c.npz